Step-by-step explanationThe general vertex-equation of a parabola has the following form:
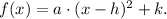
Where:
• a is a multiplicative factor,
,
• (h, k) are the coordinates of the vertex of the parabola.
In this exercise we have the following equation:
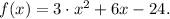
Vertex of the parabola
To find the vertex of the parabola, we will complete squares to take the equation f(x) to the general form as in the equation above.
i. We factorize the equation of f(x) in the following way:
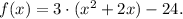
ii. Now, we rewrite the term inside the parenthesis as:
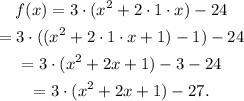
iii. Now, we see that the term in parenthesis can be rewritten as a square:
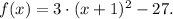
iv. Finally, we rewrite the term inside and outside the parenthesis as:
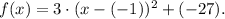
In the last step, we rewrite the term inside the parenthesis to have the same shape as in the general expression.
Comparing the equation that we have obtained and the general one, we see that the coordinates of the vertex are:
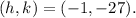
Second point
We find a second point by evaluating the function f(x) in x = 1, we get:
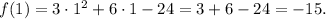
The coordinates of the second point are (1, -15).
Graph
We have the following points of the parabola:
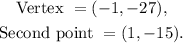
Using these points and taking into account that the axis of symmetry is x = -1 (because the x-coordinate of the vertex is -1), we get the following graph:
Answer
Coordinates of the vertex: (-1, -27)
Coordinates of the second point: (1, -15)