Question

If x squared minus 6x plus 7 equal k(2x-3) has real equal roots find the possible values of K

Answer 1

We will have the following:

`\begin{gathered} x^2-6x+7=k(2x-3)\Rightarrow x^2-6x+7=2kx-3k \\ \\ \Rightarrow x^2-6x-2kx+7+3k=0 \end{gathered}`

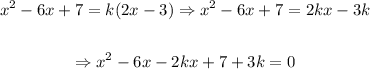
Now, we want to operate like terms and take to "solve for x" using the quadratic expression, that is:

`\Rightarrow x^2+(-6-2k)x+(7+3k)=0\Rightarrow x=(-(-6-2k)\pm√((-6-2k)^2-4(1)(7+3k)))/(2(1))`

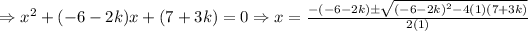
No, in order to determine the possible real values for "k" we have to analyze the value under the root, so:

`\begin{gathered} √((-6-2k)^2-4(1)(7+3k))\Rightarrow(-6-2k)^2-4(1)(7+3k)\ge0 \\ \\ \Rightarrow36+24k+4k^2-28-12k\ge0\Rightarrow8+12k+4k^2\ge0 \end{gathered}`

Now, we will have to use the quadratic expression again to determine the values for "k" that make the inequality true, that is:

`\begin{gathered} k=(-(12)\pm√((12)^2-4(4)(8)))/(2(4)) \\ \\ \Rightarrow k\leq-2 \\ \\ and \\ \\ \Rightarrow k\ge-1 \end{gathered}`

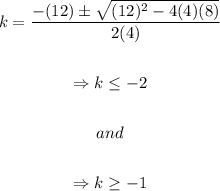
So, the values for which the inequality and thus the expression under the root are true are then given by:

`k\leq-2\wedge x\ge-1`

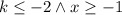
In other notation:

`(-\infty,2]\cup[-1,\infty)`