Question

The distance between two distinct points: ordered pair 1 (x , y) and ordered pair 2 (x, y) is given by the formula ____?____.(I need the formula)

Answer 1

Given an ordered pair 1:

`\mleft(x,y\mright)`

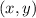
And a distinct ordered pair 2:

`(x,y)`

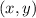
You can rewrite them as:

`\begin{gathered} (x_1,y_1) \\ \\ (x_2,y_2) \end{gathered}`

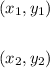
According to the Pythagorean Theorem, for Right Triangles:

`c=\sqrt[]{a^2+b^2}`

Where "c" is the hypotenuse and "a" and "b" are the legs of the Right Triangle.

Then, you can set up that:

Then, to find the hypotenuse of the Right Triangle or the distance "d" between the points, you can apply the Pythagorean Theorem and set up that:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Therefore, the answer is:

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`