Answer:
The minimum unit cost is $12,197.
Explanation:
The cost function is given below:
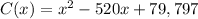
To find the minimum unit cost, first, find the derivative of C(x).
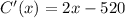
Next, set the derivative equal to 0 and solve for x.
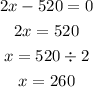
Finally, substitute x=260 into C(x) to find the minimum cost.
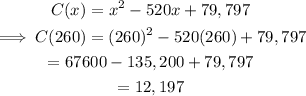
The minimum unit cost is $12,197.