Answer:
![(\sqrt[]{2\text{ }},-1)\text{ and (-}\sqrt[]{2\text{ }}\text{ ,-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/xrcftgq6gpoj5pe2a8od0h65cbngluxme8.png)
Step-by-step explanation:
Here, we want to solve the system of equations
Since we have y in both equations, let us start by rewriting the second equation to look like the first
We have that as:
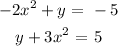
Subtract equation ii from i
We have it that:
![\begin{gathered} -5x^2=\text{ -10} \\ 5x^2=10 \\ x^2=\text{ 2} \\ \\ x\text{ = }\pm\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f70pyq8gzl8tl2x4u199i9t9v65sidmy1r.png)
when x = positive root 2, we have it that:
![\begin{gathered} -2x^2+y\text{ = -5} \\ -2(\sqrt[]{2\text{ }})^2+y\text{ = -5} \\ -4+y\text{ = -5} \\ y\text{ = -5+4} \\ y\text{ = -1} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/giu235977ugug0u0pnqg4fw75f08c71ctk.png)
when x = negative root 2:
We will still get the same answer as the square of both returns the same value
Thus, we have the solution to the system of equations as:
![(\sqrt[]{2\text{ }},-1)\text{ and (-}\sqrt[]{2\text{ }}\text{ ,-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/xrcftgq6gpoj5pe2a8od0h65cbngluxme8.png)