Let's make a graph to better understand the question:
a.) A particle starting at (1,0) and making one counterclockwise revolution on the unit
circle.
In the given description, we can assume that the center of the circle when the particle makes a revolution is at the origin (0,0). Thus, the equation of the circle that the particle will make is:
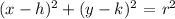
At (h,k) = (0,0) and r = distance between (0,0) to (1,0).
We get,
![(x-0)^2+(y-k)^2=(\sqrt[]{(1-0)^2+(0-0)^2})^2](https://img.qammunity.org/2023/formulas/mathematics/college/q5x4wxrhv040dz3e7kqoparrgtx44gliv6.png)
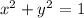
Plotting the graph,
In conclusion, there will be two points along the path of the particle that the x and y coordinate equal.
At, x = y, let's substitute this to the formula of the graph of the circle to get the coordinates.
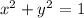
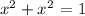
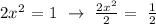
![x\text{ = }\sqrt[]{(1)/(2)}](https://img.qammunity.org/2023/formulas/mathematics/college/diycwfkpqmxp4e7t7rnszn1dn05c2npsih.png)
![x\text{ = y = }\pm\frac{1}{\sqrt[]{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/diq0uobz720xcrsek77abfx9nhc4k7vd0b.png)
Therefore, the two points where the x and y will be equal is at:
![\text{ x = y = +}(1)/(√(2))\text{ and }-\frac{1}{\sqrt[]{2}}](https://img.qammunity.org/2023/formulas/mathematics/college/l0pr7ixaroncw5jfiqu0ztk8kp1oertal3.png)