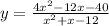Based on the question, the vertical asymptote is x = -4 and x = 3. This means the denominator cannot have these x-values or else, the function becomes undefined. Hence, from these x-values, we can say that the factors of the denominator are:
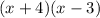
Multiplying the factors, we get:
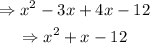
So, the denominator of our rational function must be x² + x - 12 in order to have those vertical asymptotes.
Another given information is that our x-intercepts are at x = -2 and x = 5. This means that the numerator must be zero at these x-values. Hence, we can say that some factors of the numerator are:
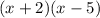
Multiplying these two factors, we get:
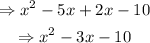
This means x² - 3x - 10 should be part of our numerator.
Another given information is that the horizontal asymptote is at y = 4. This means that the ratio between the leading coefficients of the numerator and denominator is 4. (since both have the same degree)
So, in order to have a ratio of 4, we will multiply our numerator by 4.
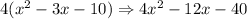
Therefore, our numerator must be 4x² - 12x - 40. And as mentioned above, the denominator must be x² + x - 12. So, the rational function is: