Step-by-step explanation
Since we have the given points:
A= (2,1)
B= (10,1)
C= (2,7)
We can represent this in a graphing calculator:
Now, in order to obtain the distance from A to B, we need to subtract both
x-coordinates points:
10-2 = 8 units
Therefore, the distance from A to B is 8 units.
Next, computing the distance from point A to the point C:
y_C - y_A = 7 - 1 = 6 units
Thus, the distance from point A to point C is 6 units.
In order to obtain the distance from the point B to C we need to apply the distance equation as shown as follows:
![\text{distance}=\sqrt[]{(7-1)^2+(10-2)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/vvfb3l4v3ebsti3smyd63mzbkl1ldaequn.png)
Subtracting numbers:
![\text{distance}=\sqrt[]{6^2+8^2}](https://img.qammunity.org/2023/formulas/mathematics/college/dpg93sold92192i723ez7dezlu69tny01g.png)
Computing the powers:
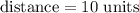
The distance from point B to point C is 10 units.
Finally, we can conclude that the given points do form a right triangle.