We will determine the maximum height of the baseball as follows:
We will need the following formulas:
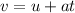
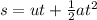
Here "u" represents the original speed, "t" represents the time, "a" the acceleration of the body and "s" is the total discance moved. [We will find s to solve the problem].
So:
First we have that the acceleation that the body will experience is -9.8m/s^2 [Since the object is going upwards and gravity is pulling on it towards the ground]. [acceleration of gravity using feet over second squared is 32.17 ft/s^2].
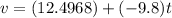
But the maximum height will be reached when the velocity after certain time has passed is 0 ft/s, so:
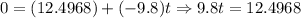
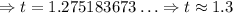
So, at approximately 1.3 seconds the maximum heigth willl be reached.
Now, we solve for s:
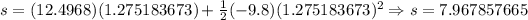
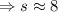
So, the maxumum altitude for the baseball will be 8 meters, but we have to add the initial 5 feet at which it was launched:
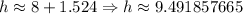
And taking that to feet we will have:
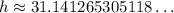
So, the solution must be the last option. [The discrepanc