Given:
a.) The circumference of a big circle is 36 pi.
b.) The area of a smaller circle located inside the bigger circle is 16 pi.
The probability that the point lands in the smaller one is,
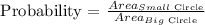
However, only the circumference of the big circle is given. To be able to get the probability, we must first determine the area of the circle.
a.) Area of the big circle.
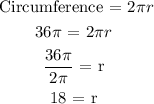

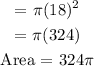
b.) Let's now determine the probability.
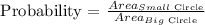
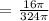
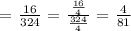
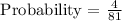
Therefore, the probability that the point lands in the smaller one is 4/81.