We are given that a spring stretches 3.02 cm vertically when a 2.5 kg object is suspended.
Part (a) To determine the constant of the spring we need first to determine the weight of the object, to do that we will use the following formula:
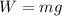
Where:
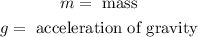
Now we plug in the values:
![W=(2.5\operatorname{kg})(9.8(m)/(s^2))]()
Solving the operations we get:

Now we use Hooke's law:
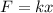
Where:
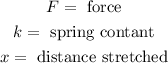
Now we solve for "k" by dividing both sides by "x":
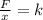
Now, since the object is placed vertically this means that the only force acting on the spring in the weight of the object, therefore:
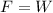
Now we plug in the known values:
![\frac{24.5N}{3.02\operatorname{cm}}=k]()
Solving the operations we get:
![8.11\frac{N}{\operatorname{cm}}=k]()
Since we are required to express the constant in N/m, we need to convert the centimeters into meters. To do that we will use the following conversion factor:
![100\operatorname{cm}=1m]()
Now we multiply by the conversion factor in decimal form, placing the centimeters as numerator:
![8.11\frac{N}{\operatorname{cm}}*\frac{100\operatorname{cm}}{1m}=811.26(N)/(m)]()
Therefore, the constant of the spring is 811.26 N/m.
part (b) Now we are asked to determine the distance is an object of 1.25 kg is place. First, we determine the weight of the new object:
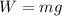
Now we plug in the values:
![W=(1.25\operatorname{kg})(9.8(m)/(s^2))=12.25N]()
Now we use Hooke's law, but we solve for the distance "x" by dividing both sides by the constant "k", we get:

Just as before, the only force acting is the weight, therefore, we plug in the values we got:
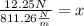
Solving the operations:

Now we convert the meters into centimeters using the same conversion factor:
![0.015m*\frac{100\operatorname{cm}}{1m}=1.5\operatorname{cm}]()
Therefore, the new mass stretches the spring 1.5 centimeters.
Part (c) Now we are asked to determine the work that has to be done on the spring to stretch it 8.9 centimeters. To determine that we will use the following formula for the work done on a spring:
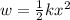
Now we replace the values:
![w=(1)/(2)(811.26(N)/(m))(8.9\operatorname{cm})^2]()
We will first convert the 8.9 centimeters into meters:
![8.9\operatorname{cm}*\frac{1m}{100\operatorname{cm}}=0.089m]()
Now we replace this in the formula for the work:
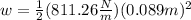
Solving the operations we get:
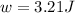
Therefore, the work is 3.21 Joules.