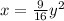Question

Find the standard form of the equation of the parabola with the given characteristic(s) and vertex at the origin.Horizontal axis and passes through the point (9, −4)

Answer 1

`x=(9)/(16)y^2`

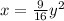
Explanation:

Since the vertex of the parabola at the origin (h,k) is (0,0). The standard form of the parabola is represented as:

`\begin{gathered} x=a(y-k)^2+h \\ \end{gathered}`

If the parabola passes through the point (9,-4), we can substitute for (x,y) and (h,k) and solve for ''a.'' and determine the equation:

`\begin{gathered} 9=a(-4-0)^2+0 \\ 9=a(16)+0 \\ a=(9)/(16) \\ \end{gathered}`

Then, the equation of the parabola in standard form would be:

`x=(9)/(16)y^2`