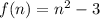Answer:
f(n)=n²-3
Step-by-step explanation:
In the sequence:
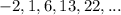
First, we find the difference between the terms.
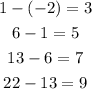
It is observed that the difference between successive terms is the addition of consecutive odd numbers.
This is an example of a quadratic sequence.
The general form of a quadratic sequence is:
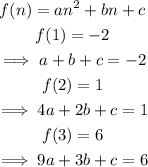
If we solve the system of equations:
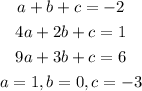
The explicit expression for this sequence is: