ANSWERS
a. 1/2
b. 1001
c. 20
d. 8
e. 0.16
Step-by-step explanation
a. There are 4 women and 4 men on the hiring committee, which is a total of 8 people. The probability that a randomly selected person is a woman is,
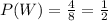
Hence, the probability that the person drawing the names from the hat is a woman is 1/2.
b. The applicant pool consists of 6 database administrators and 8 network engineers, which is a total of 14 applicants. We want to choose 4 applicants,
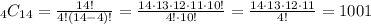
Hence, there are 1001 ways to choose the group to be hired.
c. There is a total of 6 database administrators, and we want to choose 3,
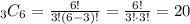
Hence, there are 20 ways of choosing 3 database administrators.
d. There is a total of 8 network engineers, and we want to choose 1,
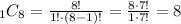
Hence, there are 8 ways of choosing 1 network engineer.
e. In part b, we found that there is a total of 1001 ways of choosing the 4 people to be hired. Also, in parts c and d, we found that there are 20 ways of choosing 3 database administrators and 8 ways of choosing 1 network engineer. The probability that this is the combination of people hired is,
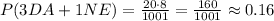
Hence, the probability that the random selection of four persons to be hired will result in 3 database administrators and 1 network engineer is approximately 0.16.