1 Answer

Vskubriev · Answer 1 · 2023-01-20T08:13:46+0000

Simplify the equation x^2 - 8x + 16 = 0 to obtain the value of x.

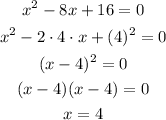
$\begin{gathered} x^2-8x+16=0 \\ x^2-2\cdot4\cdot x+(4)^2=0 \\ (x-4)^2=0 \\ (x-4)(x-4)=0 \\ x=4 \end{gathered}$

Equation has one solution, x = 4.

Simplify the equation x ( x - 1 ) = 8 to obtain the value of x.

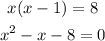
$\begin{gathered} x(x-1)=8 \\ x^2-x-8=0 \end{gathered}$

This is a quadratic equation which is not a perfect square so it has two solutions.

Simplify the equation x^2 = 16 to obtain the value of x.

$\begin{gathered} x^2=16 \\ x=\sqrt[]{16} \\ =\pm4 \end{gathered}$

Thes equation has two solution x = 4 and x = -4.

So equation x^2 - 8x + 16 = 0 has only one solution and remaining equation has two solutions.

Please log in or register to add a comment.