Question

Solve the system using the substitution technique:(−6, −3.6)(0.6, 0.8)(6, 4.4)(−0.6, 0)

Answer 1

Given

The system of equations,

`\begin{gathered} -2x+3y=1.2\text{ \_\_\_\_\_}(1) \\ -3x-6y=1.8\text{ \_\_\_\_\_}(2) \end{gathered}`

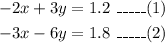
To find the solution using substitution technique.

Step-by-step explanation:

It is given that,

`\begin{gathered} -2x+3y=1.2\text{ \_\_\_\_\_}(1) \\ -3x-6y=1.8\text{ \_\_\_\_\_}(2) \end{gathered}`

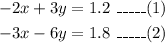
That implies,

`\begin{gathered} (1)\Rightarrow-2x+3y=1.2 \\ \Rightarrow3y=1.2+2x \end{gathered}`

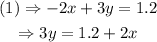
And,

`\begin{gathered} (2)\Rightarrow-3x-6y=1.8 \\ \Rightarrow-3x-2(3y)=1.8 \end{gathered}`

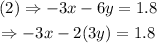
Substitute 3y=1.2+2x in the above equation.

That implies,

`\begin{gathered} -3x-2(1.2+2x)=1.8 \\ -3x-2.4-4x=1.8 \\ -7x=1.8+2.4 \\ -7x=4.2 \\ x=(4.2)/(-7) \\ x=-0.6 \end{gathered}`

And, substitute x=-0.6 in (1).

That implies,

`\begin{gathered} (1)\Rightarrow-2(-0.6)+3y=1.2 \\ \Rightarrow1.2+3y=1.2 \\ \Rightarrow3y=1.2-1.2 \\ \Rightarrow3y=0 \\ \Rightarrow y=0 \end{gathered}`

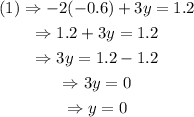
Hence, the solution is (-0.6,0).