Answer:
D
Explanation:
Given the formula of the arithmetic sequence, to find the first 5 terms, you just have to substitute n=1, n=2, n=2, n=4, and n=5.
Then, for the 1st term:
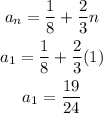
2nd term:
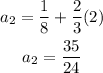
There is no need to find the other 3 because there is no other sequence that has the first two terms as D.