The formula for the z score of a number is given by:
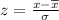
Where:
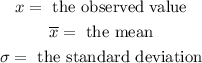
In this case,
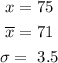
Therefore, the z score of x=75 is given by:
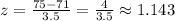
Therefore, the probability that a boy is taller than 75 inches is given by the area under the normal probability distribution curve between z=1.143 and z=∞, P(z > 1.143):
The area is approximately 0.1265.
Therefore, the required probability is 0.1265.
Convert the probability to percent by multiplying with 100:
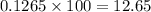
Hence, about 12.65 % of all the boys are taller than 75 inches.
Therefore, the total number of boys that are taller than 75 inches is given by:
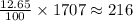
Therefore, the number of boys expected to be taller than 75 inches is approximately:
216