Question

Lottery: I buy one of 5000 raffle tickets for $1. The sponsors then randomly select one grand prize worth $500, two second prizes worth $200 each, and three third prizes at $100 each. Create the probability distribution for this raffle and calculate my expected value. Enter each row of your table as a separate line, but don't worry too much about formatting. Tables should look similar to those given in questions 1 and 3. Don't forget to give your expected value.

Answer 1

To give the probability distribution, we need to calculate the probability of each possible outcome and the value of this outcome.

We have 5000 raffle, 1 will win the first prize, 2 will win the second prize, 3 will win the third prize and the rest 4994 will win no prize.

The first prize is $500, but the raffle cost $1, so the outcome is actually $499.

The second prizes are $200 each, minus the cost we have an outcome of $199.

The third prizes are $100 each, minus the cost we have an outcome of $99.

The others will not receive prizes, but they will still have the cost of $1, so the outcome is -$1.

The first prize is 1 in 5000, so the probability is 1/5000

The second prizes are 2 in 500, so the probability is 2/5000

The third prizes are 3 in 5000, so the probability is 3/5000

The lost is the rest of the 4994 in 500, so the probability is 4994/5000

So, the table for the probability distributions is:

Value gained | P(x)

$499 | 1/5000

$199 | 2/5000

$99 | 3/5000

-$1 | 4994/5000

To calculate the expected value, we multiply the value by its probability and add them:

`\begin{gathered} E(x)=499\cdot(1)/(5000)+199\cdot(2)/(5000)+99\cdot(3)/(5000)-1\cdot(4994)/(5000)_{} \\ E(x)=(499)/(5000)+(398)/(5000)+(297)/(5000)-(4994)/(5000) \\ E(x)=(499+398+297-4994)/(5000) \\ E(x)=-(3800)/(5000) \\ E(x)=-0.76 \end{gathered}`

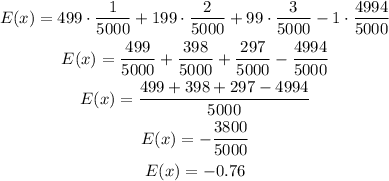
So, the expected value if -$0.76.