Question

If g(x) = f(4x), which statement is true?

Answer 1

I believe its the last answer.

Explanation:

Answer 2

The correct statement is option C.) The graph of function f is compressed horizontally by a scale factor of 1/4 to create the graph of function g.

When the expression
`\(g(x) = f(4x)\)` is used, it indicates a transformation of the original function
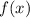`\(f(x)\)`. Specifically, the factor 4 inside the function parentheses affects the variable x. In this context, it implies a compression of the graph horizontally.

To understand this, consider that for any given x-value in function g, the corresponding x-value in function f is 1/4 of that. As a result, the entire graph of function f is squished horizontally, making it narrower.

Options A and D suggest stretching, but the correct transformation is a compression due to the multiplication by 1/4. Option B suggests a vertical compression, which is not accurate in this context.

In summary, when
`\(g(x) = f(4x)\)`, the graph of function f is compressed horizontally by a scale factor of 1/4 to create the graph of function g.