Question

Find the X-Intercept and the y-intercept of 4x- 5y = 15X-Intercept:???Y-intercept: ???help

Answer 1

The y-intercept is (0,-3) while the x-intercept is (18.75,0)

Here, we want to find the x and y-intercepts of the given line

Firstly, we have to rewrite the equation of the line in the standard form

We have this as;

`\text{y = mx + b}`

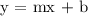
m is the slope and b is the y-intercept

Rewriting the given equation, we have this as;

`\begin{gathered} 5y\text{ = 4x-15} \\ y\text{ =}(4)/(5)x-(15)/(5) \\ \\ y\text{ = }(4)/(5)x\text{ - 3} \end{gathered}`

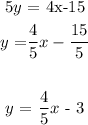
We have the y-intercept as -3

In the coordinate form, this is (0,-3)

To get the x-intercept, we set the y value to zero

We have this as;

`\begin{gathered} 0\text{ = }(4)/(5)x-15 \\ 15\text{ = }(4x)/(5) \\ \\ 4x\text{ = (15}*5) \\ 4x\text{ = 75} \\ x\text{ = }(75)/(4) \\ x\text{ = 18.75} \end{gathered}`

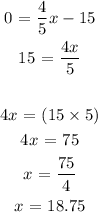
The x-intercept is 18.75 which in the coordinate form is (18.75,0)