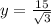Step-by-step explanation:
Consider the following right triangle:
To find the missing sides x and y, we can apply the following trigonometric ratios:
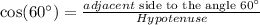
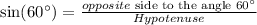
and
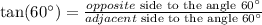
thus, applying the data of the problem to the last equation, we get:
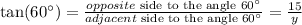
that is:
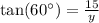
solving for y, we obtain:
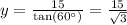
On the other hand, applying the above data to the first equation, we get:
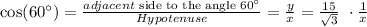
or
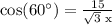
solving for x, we obtain:
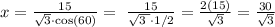
we can conclude that the correct answer is:
Answer:
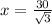
and