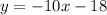anIf we have an equation of the form

then the equation of the perpendicular will be
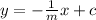
where c is any arbitrary constant determined by the point the line must pass through,
Now in our case, we have
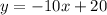
Therefore, the equation of the perpendicular line will be
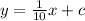
We must choose c such that the above line passes through (-2,2).
Putting in y = 2 and x = 2 from (-2, 2) gives
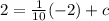
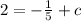
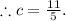
Hence, the equation of a line perpendicular y = -10x + 20 and passing through (-2, 2) is
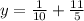
Now we find the equation of a line parallel to y = -10x+20 and passing through (-2,2).
Now, the slope of the parallel line is the same as that of the original equation; therefore the equation for the parallel line we have is
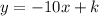
We find k by using the point (-2,2) and substituting x = -2 and y = 2 into the above equation to get
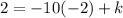


Hence, the equation of the parallel line is