Question

Determine the center and radius of the following circle equation:2² + y² – 2x – 6y – 54 = 0Center:13Radius:Submit Answer

Answer 1

Centre = (1, 3)

radius = 8units

Step-by-step explanation:

The standard equaton of a circle is expressed as;

`x^2+y^2+2gx+2fy+C\text{ = 0}`

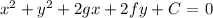
The radius of the circle is expressed as;

`r=\sqrt[]{g^2+f^2-C^{}}`

The centre is at C(-g, -f)

Given the expression;

`x^2+y^2-2x-6y-54=0`

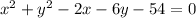
Get the centre of the circle.

Compare both equations

`\begin{gathered} 2gx=-2x \\ g\text{ = -1} \end{gathered}`

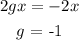
similarly;

`\begin{gathered} 2fy=-6y \\ 2f=-6 \\ f=-(6)/(2) \\ f=-3 \end{gathered}`

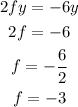
The centre will be located at C(-(-1), -(-3)) = C(1, 3)

Next is to get the radius

Recall;

`\begin{gathered} r=\sqrt[]{g^2+f^2-C} \\ r=\sqrt[]{(-1)^2+(-3)^2-(-54)} \\ r=\sqrt[]{1+9+54} \\ r=\sqrt[]{64} \\ r=8\text{units} \end{gathered}`

Hence the radius is 8units