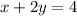We can write the line equation as:

And to find the values of the coefficients 'm', and 'b', we can use the intercepts(where the line cuts the x and y axis) on the graph. Looking at the graph, we have the following interceptions:
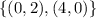
Plugging those values in our equation, we have:
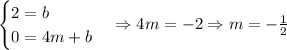
Writing the line equation in slope intercept form, we have the following:
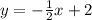
Rewriting this equation:
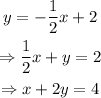
And this is our final answer. The line equation is