Question

A stack of 30 science flashcards includes a review card for each of the following 10 insects, 8 trees, 8 flowers and 4 birds. What is the probability of randomly selecting an insect and then a tree???

Answer 1

The probability (P) of event A occurring is:

`P(A)=\frac{\text{ number of favorable outcomes to A}}{\text{ total number of outcomes}}`

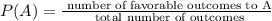
The probability of 2 consecutive events A and B occur is:

`P=P(A)*P(B)`

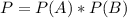
Then, let's calculate the probability of selecting an insect:

Favorable outcomes: 10

Total outcomes: 30

`P(insect)=(10)/(30)=(1)/(3)`

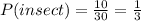
Now, let's calculate the probability of selecting tree:

If the insect card is replaced:

Favorable outcomes: 8

Total outcomes: 30

`P(B)=(8)/(30)=(4)/(15)`

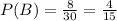
If the insect card is not replaced:

Favorable outcomes: 8

Total outcomes: 29

`P(B)=(8)/(29)`

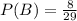
The probability of randomly selecting an insect and then a tree is:

With replacement:

`\begin{gathered} P=(1)/(3)*(4)/(15) \\ P=(4)/(45) \end{gathered}`

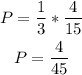
Without replacement:

`\begin{gathered} P=(1)/(3)*(8)/(29) \\ P=(8)/(87) \end{gathered}`

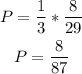
Answer:

With replacement: 4/45

Without replacement: 8/87