Question

The following data for a random sample of banks in two cities represent the ATM fees for using another bank's ATM. Compute the range and sample standard deviation for ATM feesfor each city. Which city has the most dispersion based on range? Which city has more dispersion based on the standard deviation?City A 2.50 1.50 1.25 0.00 2.00City B 1.25 1.00 1.50 1.00 1.00

Answer 1

Given:

City A: 2.50 1.50 1.25 0.00 2.00

City B: 1.25 1.00 1.50 1.00 1.00

To find dispersion based on range:

The difference between the maximum and minimum values in a set of data is the range.

2.5 is the maximum value of data of city A and 0.00 is the minimum value of data of city A.

Hence, the range of data of city A is,

`R_A=2.50-0.00=2.50`

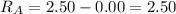
1.5 is the maximum value of data of city B and 1.00 is the minimum value of data of city B.

Hence, the range of data of city B is,

`R_B=1.50-1.00=0.50`

Since the range of city A is greater than that of city B, city A has most dispersion based on range.

To find dispersion based on the standard deviation:

The data for city A is,

2.50 1.50 1.25 0.00 2.00

The mean of city A is,

`\begin{gathered} \mu_A=(2.5+1.5+1.25+0+2)/(5) \\ =1.45 \end{gathered}`

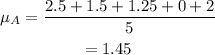
Let each individual value is represented by xi. Then, the squared difference of each individual value of city A is,

`(x_i-\mu_A)^2`

Now, find the square of difference of each individual value of city A is,

`\begin{gathered} _{}(2.5-1.45)^2=(1.05)^2=1.1025 \\ (1.5-1.45)^2=(0.05)^2=0.0025 \\ (1.25-1.45)=(-0.2)^2=0.04 \\ (0.00-1.45)^2=(-1.45)^2=2.1025 \\ (2.00-1.45)^2=(0.55)^2=0.3025 \end{gathered}`

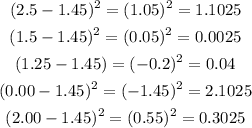
The number of values in the data set is n=5.

Let each individual value is represented by xi, then the sample standard deviation is,

`S_A=(1)/(n-1)\sum ^n_(i\mathop=1)(x_i-\mu_A)^2`

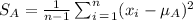
Hence, the sample standard deviation of city A can be calculated as,

`\begin{gathered} S_A=\sqrt{(1)/(5-1)(1.1025+0.0025_{}+0.04+2.1025+0.3025)}_{} \\ =\sqrt[]{(3.55)/(4)} \\ =0.9420 \end{gathered}`

Therefore, the sample standard deviation of city A is 0.9420.

The data for city B is:

1.25, 1.00, 1.50, 1.00, 1.00

The mean of city B is,

`\begin{gathered} \mu_B=(1.25+1.00+1.50+1.00+1.00)/(5) \\ =1.15 \end{gathered}`

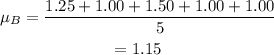
Let each individual value is represented by xi. Then, the squared difference of each individual value of city B is,

`\begin{gathered} (x_i-\mu)^2 \\ (1.25-1.15)^2=0.1^2=0.01 \\ (1.00-1.15)^2=(-0.15)^2=0.0225 \\ (1.5-1.15)^2=(0.35)^2=0.1225 \\ (1.00-1.15)^2=(-0.15)^2=0.0225 \\ (1.00-1.15)^2=(-0.15)^2=0.0225 \end{gathered}`

The number of values in the data set is n=5.

Let each individual value is represented by xi, then the sample standard deviation of city B is,

`S_B=(1)/(n-1)\sum ^n_(i\mathop=1)(x_i-\mu_B_{})^2`

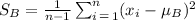
Hence, the sample standard deviation of city B can be calculated as,

`\begin{gathered} S_B=\sqrt[]{(1)/(5-1)(0.01+0.0225_{}+0.1225+0.0225+0.0225)}_{} \\ =\sqrt[]{(0.2)/(4)} \\ =0.2236 \end{gathered}`

Therefore, the sample standard deviation of city B is 0.2236.

Since the standard deviation of city A is greater than that of city B, city A has more dispersion based on the standard deviation.