Given:
The monthly cost is 37 min is $13.21
70 min cost is $17.50
Find-:
The monthly cost for 45 minutes of calls
Explanation-:
The linear equation is:
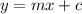
Where,
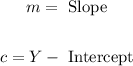
The formula of the slope is:

The point is:
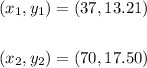
So, the slope is:
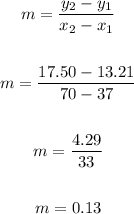
Slope is:
The general equation of a line:
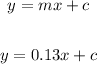
The value of "c" is:
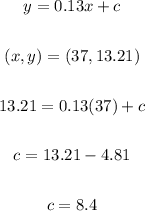
The equation is:
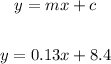
Cost at 45 min. is:
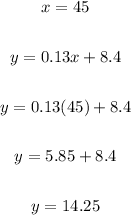
The 45 min cost is $14.25