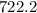Answer:
The minimum (cut off) score you need to receive this award is;
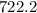
Step-by-step explanation:
Given that the top 3% of the students receive a $500 prize.
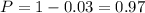
We will then find the z-score that corresponds to the given probability.

Recall that;
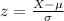
Given;
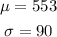
substituting the values;
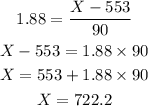
Therefore, the minimum (cut off) score you need to receive this award is;