Question

Hi I need help solving for each of the sides in this equation.CDABSolve to the nearest hundredth

Answer 1

Step-by-step explanation

Length of CD

From the picture, we know two sides and an angle of the triangle CDE. We define the sides and angle:

• a = EC = 440.68,

,

• b = ED = 470.43,

,

• c = CD = ?,

,

• γ = 60° 06' 09''.

From trigonometry, we know that the Law of Cosines states that:

`\begin{gathered} c^2=a^2+b^2-2ab\cdot\cos\gamma, \\ c=√(a^2+b^2-2ab\cdot\cos\gamma). \end{gathered}`

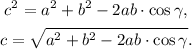
Where the angle γ and the sides a, b and c are defined by:

Replacing the values from above in the equation for side c, we get:

`c=\sqrt{(440.68)^2+(470.43)^2-2\cdot440.68\cdot470.43\cdot\cos(60\degree06^(\prime)09^(\prime)^(\prime))}\cong457.10.`

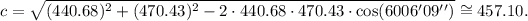
Length of AB

To compute the length of AB, first, we must compute the length of sides AE and EB.

Side EB

From the picture, we see a triangle ECA. Using the data of the picture, we have:

• EC = 440.68,

,

• ∠E = 60° 06' 09'',

,

• EA = ?,

,

• ∠A = ?.

,

• ∠C = 97° 17' 42''.

Angles ∠A, ∠E and ∠C are the inner angles of triangle ECA, so they must sum up 180°, so we have:

`\begin{gathered} ∠A+∠E+∠C=180\degree, \\ ∠A=180\degree-∠E-∠C, \\ ∠A=180\degree-60\degree06^(\prime)09^(\prime\prime)-97\degree17^(\prime)42^(\prime\prime)=22°36^(\prime)9^(\prime\prime). \end{gathered}`

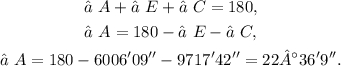
Now, we define the following sides and angles:

• c' = EC = 440.68,

,

• γ' = ∠A = 22° 36' 9''

,

• a' = EA = ?,

,

• α = ∠C = 97° 17' 42''.

Now, from trigonometry, we know that the Law of Sine states that:

Using the equation that relates a' and c', we have:

`\begin{gathered} (a^(\prime))/(\sin\alpha^(\prime))=(c^(\prime))/(\sin\gamma^(\prime)), \\ a^(\prime)=c^(\prime)*(\sin\alpha^(\prime))/(\sin\gamma^(\prime)). \end{gathered}`

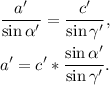
Replacing the values from above, we get:

`EA=a^(\prime)=440.68*(\sin(97°17^(\prime)42^(\prime\prime)^))/(\sin(22°36^(\prime)9^(\prime\prime)))`

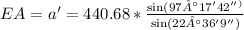
Side AE

From the picture, we see a triangle EDB. Using the data of the picture, we have:

• b' = ED = 470.43,

,

• ∠E = 60° 06' 09'',

,

• a' = EB = ?,

,

• α' = ∠D = 180° - 87° 20' 24'' = 92° 39' 36'',

,

• β' = ∠B = 180° - ∠D - ∠E = 180° - 92° 39' 36'' - 60° 06' 09'' = 27° 14' 15''.

Applying the law of sines, we have that:

`\begin{gathered} (a^(\prime))/(\sin(\alpha^(\prime)))=(b^(\prime))/(\sin(\beta^(\prime))), \\ EB=a^(\prime)=b^(\prime)*(\sin(\alpha^(\prime)))/(\sin(\beta^(\prime))). \end{gathered}`

Replacing the values from above, we get:

s

Answer

s