Given:

To Determine: The probability that a randomly selected customer will have to wait less than 21 minutes, to the nearest thousandth
Solution
Using normal distribution formula below
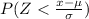
Substitute the given into the formula
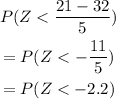
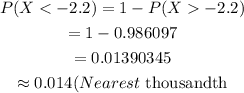
Hence, the probability that a randomly selected customer will have to wait less than 21 minutes, to the nearest thousandth is 0.014