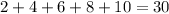Question

Find the sum of 5 even positive integers

Answer 1

sum of 5 even positive integers

`n+(n+2)+(n+4)+(n+6)+(n+8)`

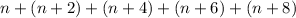
here, n is the first even number,

let's simplify this,

`\begin{gathered} =n+n+2+n+4+n+6+n+8 \\ =5n+20 \end{gathered}`

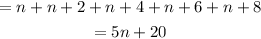
Thus the expression to find the sum of 5 consecutive even positive integers is, 5*n + 20 , where n is the 1st even positive integer.

let's use it when n = 2 or to sum 2, 4, 6, 8 and 10

`5*2+20=10+20=30`

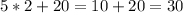
which is the same as,

`2+4+6+8+10=30`