SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given ratios
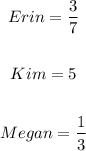
STEP 2: Add the ratios
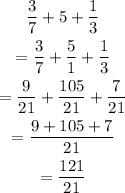
STEP 3: Calculate the earnings of each of them
Erin's
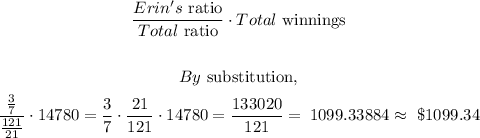
Kim's
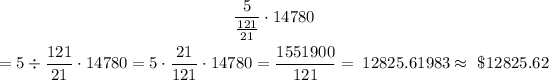
Megans's
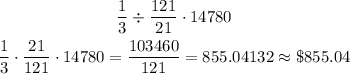
Hence, the earnings are given as:
Erin's: $1099.34
Kim's: $12825.62
Megan's: $855.04