Question

Question attached as screenshot below: please help me Pre Calculus

Answer 1

From the given question

The volume of a cone is:

`V=(1)/(3)*\pi* r^3`

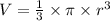
Now,

We are given with radius and the height of the cone

So,

We can solve for the radius as a function of water level using ratio and proportion

Then,

`\begin{gathered} (3)/(9)=(r)/(h) \\ r=(h)/(3) \end{gathered}`

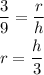
Substitute the value of r into the above formula

So,

`\begin{gathered} V=(1)/(3)*\pi* r^3 \\ V=(1)/(3)*\pi*((h)/(3))^3 \\ V=(h^3)/(81)*\pi \end{gathered}`

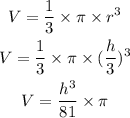
Then,

Taking derivatives

`\begin{gathered} V=(h^3)/(81)*\pi \\ (dV)/(dt)=(h^3)/(81)*\pi \end{gathered}`

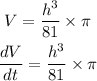
The,

Solving for the dh/dt

So,

`\begin{gathered} (dV)/(dt)=10\text{ and h=3, then } \\ (dh)/(dt)=9.55m\text{ /s} \end{gathered}`

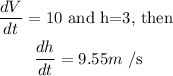
Hence, the answer is 9.55.