Question

the dealer in a card game draws three cards from a deck of 52 cards and places them face-up on the table select all the correct probabilities

Answer 1

Step-by-step explanation:

nCx give us the number of ways in which we can select x cards from a group of n cards.

So, the number of ways in which we can select 3 cards from 52 is:

52C3.

On the other hand, the number of ways to select 3 cards but none of them are kings is 48C3 because there are 48 cards that aren't kings. So:

`P(no\text{ Kings)=}(_(48)C_3)/(_(52)C_3)`

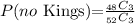
The number of ways to draw 2 fives is: 4C2*48C1

Because the dealer needs to draw 2 cards from the 4 that are fives and 1 card from the other 48 cards. So, P(2 fives) is:

`P(\text{ 2 fives)=}(_4C_2*_(48)C_1)/(_(52)C_3)`

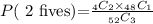
The number of ways to draw 1 heart and 2 spades is: 13C1*13C2

Because there are 13 heart cards and 13 spades cards. So, P(1 heart and 2 spades) is:

`P(1\text{ Heart and 2 spades) = }\frac{_(13)C_1*_(13)C_2_{}}{_(52)C_3}`

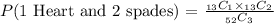
Finally, the number of ways to select 4 aces and 1 ten is