Question

The function y=f(x) is graphed below. Plot a line segment connecting the points on ff where x=-8 and x=-5. Use the line segment to determine the average rate of change of the function f(x) on the interval −8≤x≤−5.

Answer 1

`\begin{gathered} \triangle y=-10 \\ \triangle x=3 \\ Average\text{ rate of change}=-(10)/(3) \end{gathered}`

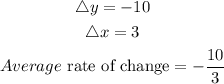
Explanations:

The formula for calculating the rate of change of a function is expressed as:

`f^(\prime)(x)=(f(b)-f(a))/(b-a)`

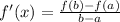
Using the connecting points x = -8 and x = -5 on the graph, this means:

a = -8 = x1

b = -5 = x2

f(b) is f(-5) which is the corresponding y-values at x = -8

f(a) is f(-8) which is the corresponding x-values at x = -5

From the graph;

f(b) = f(-5) = -20 = y2

f(a) = f(-8) = -10 = y1

Determine the change in y and change in x

`\begin{gathered} \triangle y=y_2-y_1=-20-(-10) \\ \triangle y=-20+10=-10 \\ \triangle x=x_2-x_1=-5-(-8) \\ \triangle x=-5+8=3 \end{gathered}`

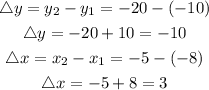
Find the average rate

`\begin{gathered} Average\text{ rate of change}=(f(b)-f(a))/(b-a)=(\triangle y)/(\triangle x) \\ Average\text{ rate of change}=-(10)/(3) \end{gathered}`

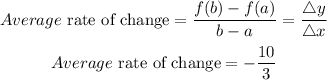
For the grah , draw a line connecting the coordinate point (-5, -20) and (-8, -10)