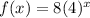Question

Find the exponential equation that goes through the points (-1, 2) and (2, 128) Bullet point 3

Answer 1

The general form of the exponential function is given by;

`y=f(x)=ab^x`

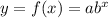
where a is the initial value and b is any value greater than 0.

If the exponential function goes through the points (-1, 2) and (2, 128) we have;

`2=ab^(-1)\ldots\ldots\ldots\text{.}.1`

And,

`128=ab^2\ldots\ldots\ldots\text{.}.2`

Divide [2] by [1] we have;

`(128)/(2)=(ab^2)/(ab^(-1))`

Simplify

`\begin{gathered} 64=(b^2)/(b^(-1)) \\ 64=b^2/ b^(-1) \\ 64=b^(2--1) \\ 64=b^(2+1) \\ 64=b^3 \end{gathered}`

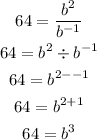
Find the cube-root of both sides

`\begin{gathered} \sqrt[3]{64}=\sqrt[3]{b^3} \\ 4=b \\ \therefore b=4 \end{gathered}`

Substitute the value of b = 4 in [2] we get;

`\begin{gathered} 128=ab^2 \\ 128=a(4)^2 \\ 128=16a \\ \text{Divide both sides by 16} \\ (128)/(16)=(16a)/(16) \\ 8=a \\ \therefore a=8 \end{gathered}`

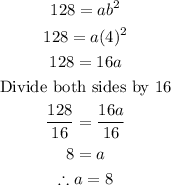
Substitute the value of a and b in

`f(x)=ab^x`

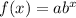
then we have;

`f(x)=8(4)^x`

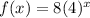
Therefore, the exponential function that goes through the points ( -1, 2) and (2, 128) is;

`f(x)=8(4)^x`