Given the word problem, we can deduce the following information:
1. Reshanda bought 17 plants to arrange along the border of her garden.
2. The plants are comprised of 6 tulips, 5 roses, and 6 daisies.
To determine the distinct arrangements that can she make, we use permutation as it an arrangement of objects in a definite order. The process is shown below:
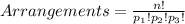
where:
n=number of different objects=17
p1=objects of the first kind=6
p2=objects of the second kind=5
p3=objects of the third kind=6
We plug in what we know:

Therefore, the answer is 5717712 arrangements.