Question

Can someone help with algebra 2?

Answer 1

The given function is

`f(x)=\begin{cases}(1)/(3)x+1\colon x<-2 \\ x-3\colon-1\leq x<2 \\ 3\colon x\ge2\end{cases}`

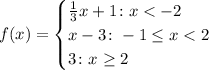
A piecewise function is a function that behaves differently on each interval. In this case, we have three intervals with three different behaviors, so let's graph each of them.

First part. 1/3x + 1.

We have to find coordinated points for the values x = -4 and x = -3. To do so, we have to evaluate the expression for each value.

`\begin{gathered} (1)/(3)\cdot(-4)+1=-(4)/(3)+1=(-4+3)/(3)=-(1)/(3) \\ (1)/(3)\cdot(-3)+1=-1+1=0 \end{gathered}`

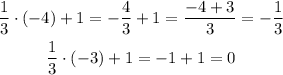
So we have two points for the first expression: (-4, -1/3) and (-3, 0).

Second part. x - 3.

Let's evaluate the expression for x = -1 and x = 0.

`\begin{gathered} -1-3=-4 \\ 0-3=-3 \end{gathered}`

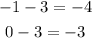
The points are (-1, -4) and (0, -3).

For the third part, we don't have to evaluate any expression because the function, in that interval, is a horizontal line.

Now, we just have to graph all the points on the same coordinated plane, as the image below shows.