Given data
*The given veloicty of the rock is u = 27 m/s
*The given height of the cliff is h = 35 m
*The given height of the Rick from the ground level is s = 5 m
*The value of the acceleration doue to gravity is g = 9.8 m/s^2
The formukla for the time taken by the Rick at 5 meters from the ground level is given as
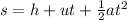
Substitute the known values in the above expression as
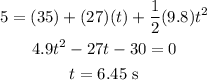
Hence, the time taken by the Ric at 5 meters above the ground lel is t = 6.45 s