The logarithmic expression is
 and the value is w = 1.71
and the value is w = 1.71
How to solve the equation for w
From the question, we have the following parameters that can be used in our computation:
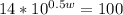
Divide both side by 14
So, we have
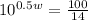
Take the logarithm of both sides
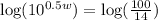
So, we have
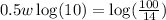
The log of base 10 is 1
So, we have
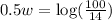
Divide both sides by 0.5

When the expression is evaluated, we have
w = 1.71
hence, the expression is
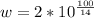 and the value is w = 1.71
and the value is w = 1.71