Given:
an equation is given as m² -5m - 14 = 0
Find:
we have to solve the given quadratic equation.
Step-by-step explanation:
Compare the given equation with am² + bm + c = 0, we get
a = 1, b = -5, c = -14
we will solve the given equation as following
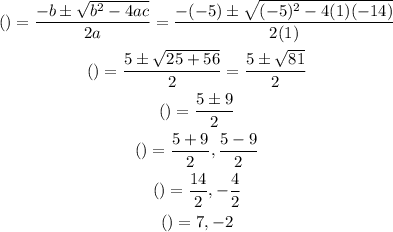
Therefore, the solution of given equation is m = 7, -2