We have an hemisphere (a shape that is half a sphere) of radius r = 7 ft, that is a bowl filled with water up to a depth of 2 ft.
We have to find at what angle must it be tipped for the water begind to flow. We have to take into account that the level of the water will remain horizontal when we tip the bowl.
This will happen when the water level reaches the edge of the hemisphere.
This can be represented as:
The bowl have to be tipped so the edge descends 2 ft.
We can represent that in mathematical terms as:
Then, we can relate the angle with the depth using a trigonometric ratio:
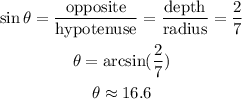
Answer: the angle is 16.6°