Question

The sum of two numbers is 200 and their difference is 28.What are the two numbers?

Answer 1

Let us assume the numbers are x and y.

The first part of the question can be written as

`x+y=200\text{ ---------------(1)}`

and the second part can be written as

`x-y=28\text{ --------------(2)}`

From equation 1, we can get a value for y as

`y=200-x\text{ -------------(3)}`

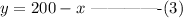
Substitute for y in equation 3 into equation 2:

`x-(200-x)=28`

Expanding and solving, we get

`\begin{gathered} x-200+x=28 \\ 2x=200+28 \\ 2x=228 \\ \therefore \\ x=(228)/(2) \\ x=114 \end{gathered}`

Next, we substitute for the value of x into equation 3:

`\begin{gathered} y=200-114 \\ y=86 \end{gathered}`

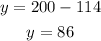
Therefore, the two numbers are 114 and 86