Question

Find each probability of the events and place them in order

Answer 1

Considering Box A,

Total number of pens = 3 + 5 = 8 pens

Probability of picking a purple (P) and black (B) pen is given below as,

`\begin{gathered} P(P)=(3)/(8) \\ P(B)=(5)/(8) \end{gathered}`

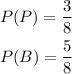
Considering Box B,

Total number of pens = 15 + 5 = 20 pens

Probability of picking a purple and black pen is given below as,

`\begin{gathered} P(P)=(15)/(20) \\ P(B)=(5)/(20) \end{gathered}`

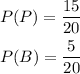
For event 1, probability of choosing a red (R) pen from Box B is zero because there is no red pen in the Box.

Event 1 P(R) = 0

For event 2, probability of choosing a purple or black pen from Box A is,

`P(P\text{ or B)=}(3)/(8)+(5)/(8)=(3+5)/(8)=(8)/(8)=1`

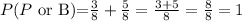
Event 2 P(P or B) = 1

For event 3, probability of choosing a purple pen from Box A is,

`P(P)=(3)/(8)`

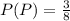
Event 3 (P) = 3/8

For event 4, probability of choosing a black pen from Box B is given below as,

`P(B)=(5)/(20)=(1)/(4)`

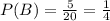
Event 4 P(B) = 1/4

Arranging each events from the least likely to the most likely is in the order below

`\text{Event 1, Event 4, Event 3, Event 2}`

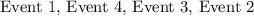
Answer deduced above.