Let:
x be the liters of 20% acid solution.
y be the liters of pure acid solution.
To find x and y, follow the steps below.
Step 01: Write an equation for the number of liters.
The number of liters of the solution is 44, which is the sum of x and y.
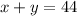
Step 02: Isolate y in the equation above.
To do it, subtract x from both sides.
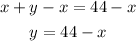
Step 03: Write an equation that expresses the total of acid.
The total of acid is 0.4*44, which is equal to 1y plus 0.2x.
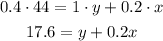
Step 04: Substitute y by 44 - x in the equation above and isolate x.
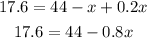
To isolate x, subtract 44 from both sides.

Now, divide both sides by -0.8.

Step 05: Use the equation from step 2 to find y.
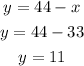
Answer:
x is the liters of 20% acid solution = 33 L.
y is the liters of pure acid solution = 11 L.