Solution
Area of square base of sides x is
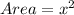
Volume = 4000cm^3
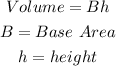
Thus,
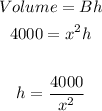
For the box to require the least possible material, is to simply minimize the surface area of the rectangular box
The surface Area is given as
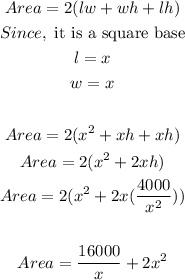
Now, we differentiate
![\begin{gathered} Area=(16,000)/(x)+2x^(2) \\ A=16000x^(-1)+2x^2 \\ By\text{ differentiating} \\ (dA)/(dx)=-16000x^(-2)+4x \\ \\ At\text{ minimum area, }(dA)/(dx)=0 \\ 4x=16000x^(-2) \\ x^3=4000 \\ x=10\sqrt[3]{4} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/oqnbaquab0g8sbvmevngvypizla526zr9p.png)
Now, to find h
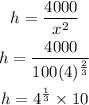
Therefore,
![\begin{gathered} Length=10\sqrt[3]{4}cm=15.874cm\text{ \lparen to three decimal places\rparen} \\ Width=10\sqrt[3]{4}cm=15.874cm\text{ \lparen to three decimal places\rparen} \\ height=15.874cm\text{ \lparen to three decimal places\rparen} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tcwqxwegzeq4mcd2anwnw4prl2p4zxoodc.png)