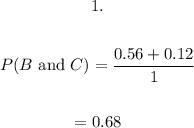Given:
The graph is:
Find-:
(a)
Find the probability that a real number between 4 and 6 is picked.
(b)
Find the probability that a real number between 4 and 7 is picked.
Explanation-:
The area of the region
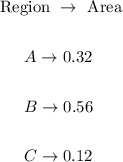
The probability is:
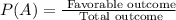
The total outcomes is:
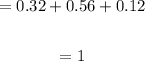
(a)
Probability to the 4 and 6
The 4 to 6v region is B

(B)
Probability for 4 to 7
The region B and C