Producing cost:
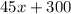
Revenue:
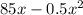
The profit (P) is equal to substract the producing cost for the revenue:
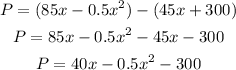
You can write also as:
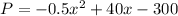
----------------------------------
P=50:
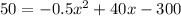
To solve for x:
Substract 50 in both sides of the equation:
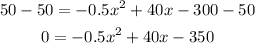
Use the quadratic formula:
![\begin{gathered} ax^2+bx+c=0 \\ \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/7aff8mm3mfsnzv3fikx7rosnjx11m76p6i.png)
![\begin{gathered} x=\frac{-40\pm\sqrt[]{40^2-4(-0.5)(-350)}}{2(-0.5)} \\ \\ x=\frac{-40\pm\sqrt[]{1600-700}}{-1} \\ \\ x=\frac{-40\pm\sqrt[]{900}}{-1} \\ \\ x=(-40\pm30)/(-1) \\ \\ x_1=(-40+30)/(-1)=(-10)/(-1)=10 \\ \\ x_2=(-40-30)/(-1)=(-70)/(-1)=70 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dq902cy25kvyhao1nltb2m5rbppkvzq4rk.png)
Then, the two values of x that make a profit of $50 are: 10 and 70
------------------ ----------------------
P=2500
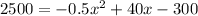
Solve for x:
![\begin{gathered} 0=-0.5x^2+40x-300-2500 \\ 0=-0.5x^2+40x-2800 \\ \\ x=\frac{-40\pm\sqrt[]{40^2-4(-0.5)(-2500)}}{2(-0.5)} \\ \\ x=\frac{-40\pm\sqrt[]{1600-5000}}{-1} \\ \\ x=\frac{-40\pm\sqrt[]{-34000}}{-1} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ile6m4gmjlgt83z5mg2c1eedj7sjqpvpux.png)
As the number under the square root is a negative number the equation has no solution (value of x) in the real numbers.
No, is not possible for the company to make a profit of $2500