Solution
We are given that
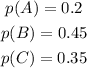
Note 1: Probability Formula To use
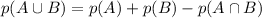
Note 2: Team A, B and C are Mutually Exclusive
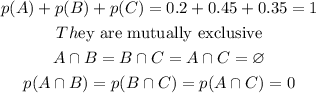
Therefore, the formula to use now is
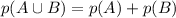
For Anna
Anna can join either team A or team B.
We calculate the probability
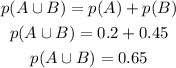
For Elina
Elina can join either team B or team C.
We calculate the probability
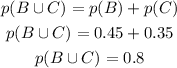
For Nancy
Nancy can join either team A or team C.
We calculate the probability
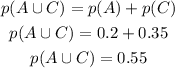
The one with the highest probability is most likely to win and that is
ELINA
Correct answer is Elina